“モンティ・ホール問題”を解き明かして数学的思考力を養ってみないか? 小学生でもわかるような丁寧な説明に「そうだったのか」と納得が止まらない
今回紹介する、カネヨシさんが投稿した『とても分かりやすい「モンティホール問題」【ゆっくり解説】』という動画では、音声読み上げソフトを使用して、モンティホール問題について解説していきます。
投稿者メッセージ(動画説明文より)
こんにちは。カネヨシです。
ふと思い立ってモンティホール問題の解説をすることにしました。この問題は中学生の頃の数学の教科書に記載されていたと記憶しています。この動画では、当時私が毎日考えた結果、自分なりに納得できた考え方を説明しています。
また、Twitterのアイコンにもしているイラストの自慢も兼ねて、少しだけ立ち絵を動かしてみました。
動画制作のために日曜日を丸々使ったので最後まで視聴してくださると嬉しいです。

カネヨシ:
カネヨシです。まずはモンティホール問題とは何かを説明していきます。プレイヤーの前に閉じた3つのドアがあって、一つのドアの後ろには景品の新車が、二つのドアの後ろには、ハズレを意味するヤギがいます。

プレイヤーは新車のドアを当てると新車がもらえます。プレイヤーが一つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せます。ここでプレイヤーは、最初に選んだドアを残っている開けられていないドアに変更しても良いと言われます。ここでプレイヤーはドアを変更すべきでしょうか。
答えは「ドアを変更すべきである」です。直感で正しいと思った答えと論理的に正しい答えが違うという点が、この問題をとても有名にしました。
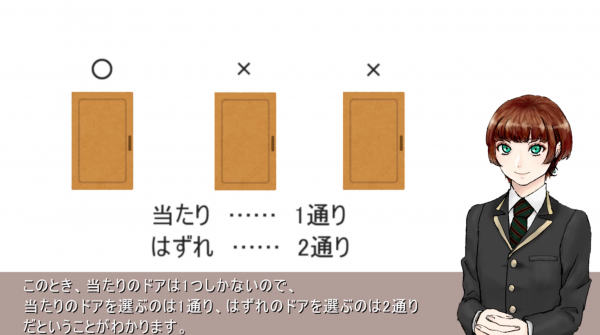
まず、プレイヤーは三つのドアから一つのドアを選びます。この場合、プレイヤーが選んだドアは、ハズレが、あるいは当たりかのどちらかですね。この時、当たりのドアは一つしかないので、当たりのドアを選ぶのは一通り、ハズレのドアを選ぶのは二通りだということが分かります。

次に場合分けをして見ましょう。先に、プレイヤーがあたりを選んでいた場合を考えます。司会は残り二つのドアのうちドア一つを開きます。プレイヤーが選んだのは当たりのドアなので、残りのドアはどちらもハズレです。
つまり、プレイヤーがあたりを選んでいた場合、ドアを変更するとハズレになり、変更しないとあたりになることが分かります。

今度はプレイヤーがハズレを選んでいた場合を考えます。プレイヤーが選んだのはハズレのドアなので、残りのドアのうち一方が外れ、もう一方が当たりです。司会はこのうちハズレの方を開けます。司会が開けなかったドアはあたりです。
つまり、プレイヤーがハズレを選んでいた場合、ドアを変更すると当たりになり、変更しなければハズレになることが分かります。一見すると変更しなくてもプレイヤーが選んでいたものによって当たりハズレが変わるのだから、確率は変わらないように思えます。
しかし、ここで大切なのはプレイヤーがハズレのドアを選ぶのが二通りであるということです。
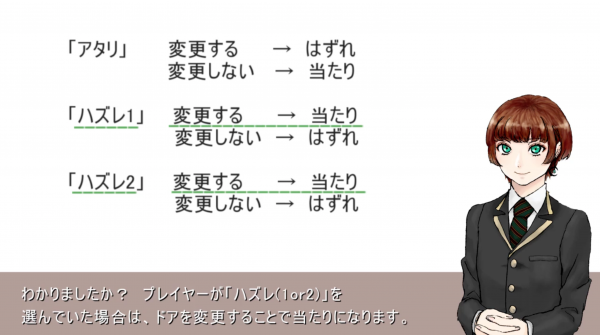
ここで分かりやすく、三つのドアをそれぞれ「アタリ」「ハズレ」「ハズレ2」と名付けることにします。プレイヤーが「アタリ」を選んでいた場合、変更するとはずれ、変更しないと当たり。プレイヤーが「ハズレ1」を選んでいた場合、変更すると当たり、変更しなければハズレ。そしてプレイヤーが「ハズレ2」を選んでいた場合、変更すると当たり、変更しないとハズレ。
分かりましたか? プレイヤーが「ハズレ(1or2)」を選んでいた場合は、ドアを変更すると当たりになります。そしてプレイヤーが「ハズレ(1or2)」を選んでいる確率は、3分の2です。

つまり、ドアを変更して当たりになる確率は、プレイヤーが「ハズレ(1or2)」を選ぶ確率と等しく、3分の2です。ドアを変更しないで当たりになる確率は、プレイヤーが「アタリ」を選ぶ確率と等しく、3分の1。したがって、ドアを変更したほうが当たりになる確率が高いことが分かります。
ドアを変更することで、ドアを変更しないで当たりになる確率である3分の1から、ドアを変更して当たりになる確率である3分の2に確率をあげることが出来ます。つまりは、ドアを変更すると当たりになる確率が2倍になります。
よって、これらのことからプレイヤーはドアを変更すべきだという答えが導かれます。
モンティ・ホール問題という答えの導き出しを解説をして理解することが出来ました。解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
▼動画をノーカットで楽しみたい方は
こちらから視聴できます▼
―あわせて読みたい―
・“最強の関数”ってナンだ!? 数式ごとに項を比較して強さを決める動画が登場。n次関数vs指数関数、指数関数vs階乗関数…バトルの結果に視聴者も謎の納得