“偏差値”ってどうやって決まるか知ってる? 中学数学を使ってわかりやすく解説。平均点を取ると「50」になるのには視聴者もビックリな理由があった
今回紹介するのは、Yoideaさんが投稿した『中学数学でわかる偏差値の意味と計算【受験生必見】』という動画です。
投稿者メッセージ(動画説明文より)
偏差値とは何者なのか、中学数学のみで計算方法と意味について話しました。
模試の成績を有効活用するためや、成績を説教の材料にされたときの反論のための知識としてお使い下さい。
テストの点数以外にも活用できる統計の基礎知識です。


中学数学だけで偏差値がどのように求められているのかを解説していきます。
この知識があると偏差値を説教の判断材料にされたときに、一方的に言われなくて済みます。

まずは良い点と悪い点を考えていきます。
例えば、上記の表のようなテスト結果があったとします。この表をみると、佐藤が良さそうだと分かります。また高橋が悪そうということも分かります。しかし、伊藤はどうなのかと言われると何とも言えません。
そこで平均値という値を使います。この結果で平均すると、平均点は60点ということが分かります。
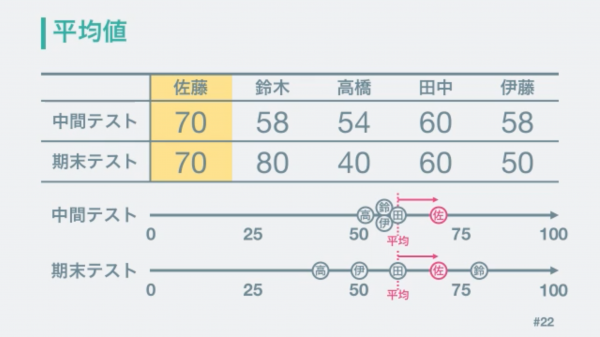
全員のテスト結果を見てみましょう。佐藤は中間テスト、期末テストともに、平均点より10点高いことが分かります。
しかし、点数の散らばり方は中間テストは小さく、期末テストは大きいことが分かります。その為、中間テストでの10点差は大きな価値を持っていて、期末テストは同じ10点差でも価値が価値が小さいです。
分かりやすい平均点の解説に「図が直感的で分かりやすい」といった称賛する意見が寄せられました。
散らばりを計算して数値化
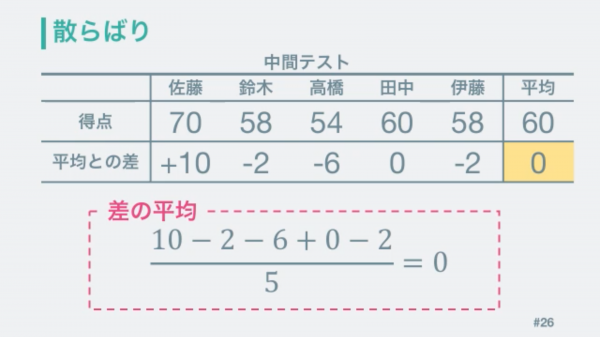
そこで、この散らばりを数値で表す方法を考え出されました。それぞれの点が平均よりどれぐらい離れてるかをまとめます。それぞれの差の平均を求めてみると0になります。
これでは使えないので、差を二乗して全てプラスになるように計算します。
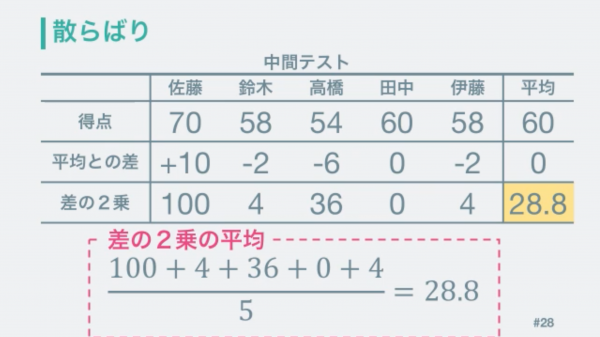
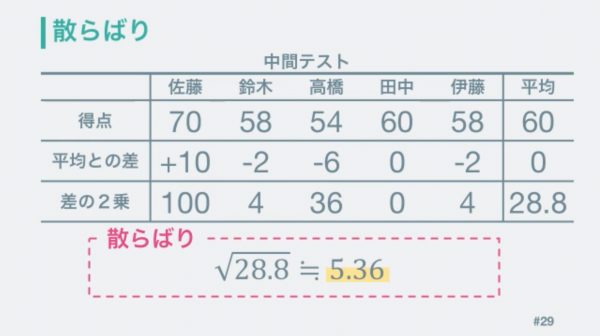
これを平均すると値を得ることが出来ました。この値は二乗したものなので平方根を計算して戻します。
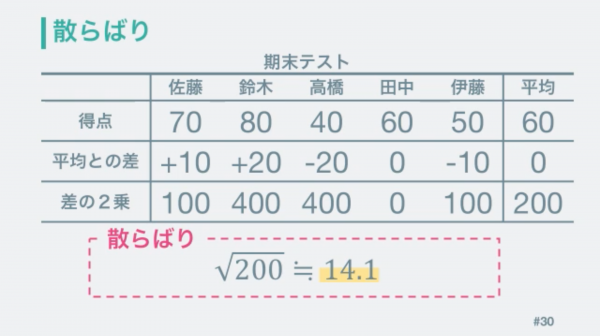
同じように期末テストも計算していきます。
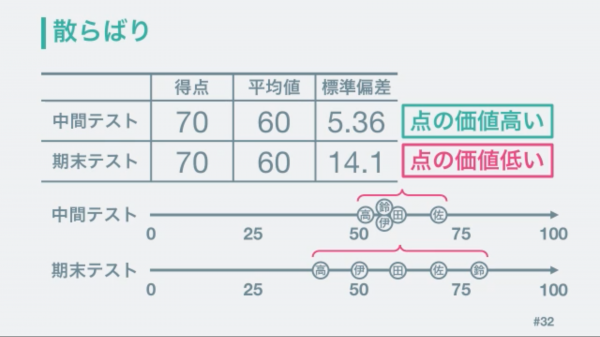
この散らばりの平均には名前がついていて専門的には「標準偏差」と言います。
中間テストは標準偏差が小さいので1点の価値が高く、期末テストは標準偏差が大きいので1点の価値が低い。
だから、同じ点差でも中間テストの得点の方が優れているといった判断が出来ます。
3つの値から判断する偏差値
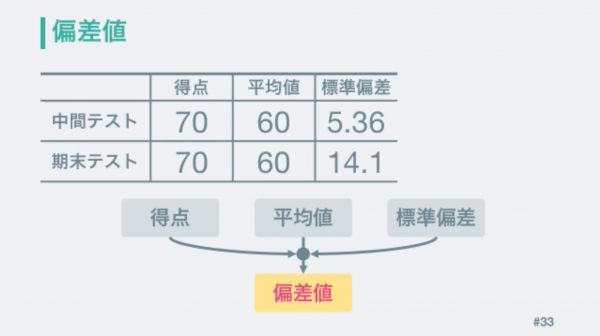
得点と平均値と標準偏差の3つの値が分かると、得点がどのくらい良いのか悪いのかを判断できます。しかし、3つの値を比べるのは面倒なので、3つの値から得点を判断できるようにしました。
それが「偏差値」という値です。

偏差値は良い成績の時に大きな値になって欲しいので、まずは得点と平均点の差を計算します。こうすると平均点を超えるとプラスの値。平均点を下回るとマイナスの値になります。
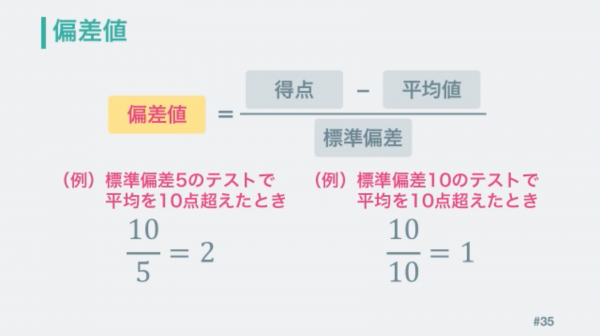
さらに、散らばりが大きいテストでは点差の価値が小さくなって欲しいので、標準偏差で割ります。
すると、標準偏差が小さいと大きな値に、標準偏差が小さいと大きな値になります。
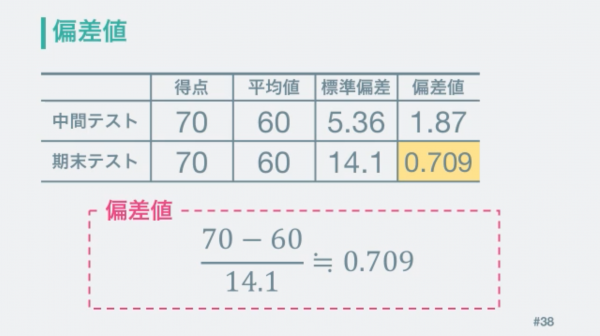
実際に代入して計算してみると、このようになります。知っている偏差値と違うと感じたかもしれません。
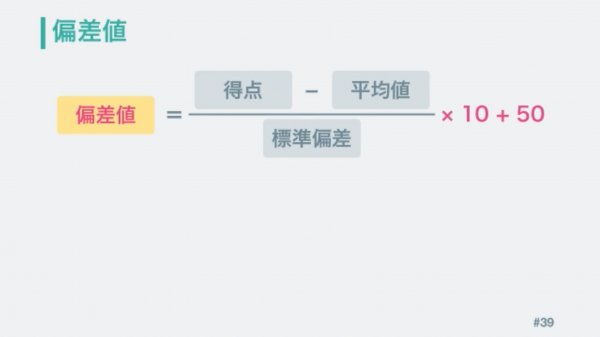
一般的に模試の結果などで使われる偏差値は、この値を10倍して50を足したものが使われます。直感的にわかりやすそうな値になるからというそれだけの理由です。
模試などに使われる偏差値の理由にコメント欄では「見やすさ重視やったんやね」「この10倍して50を足す意味だけずっとわからなかった」などといった意見が寄せられました。
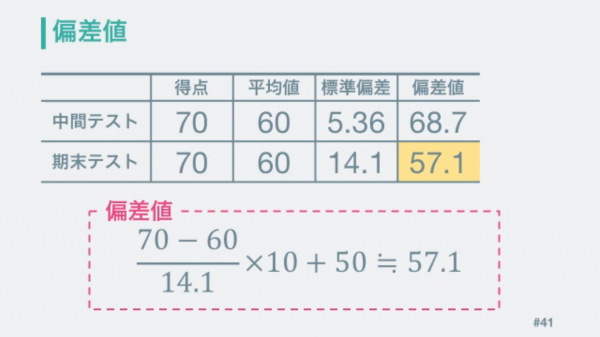
この方法で計算すると、よく知ってるような値がまとまりました。
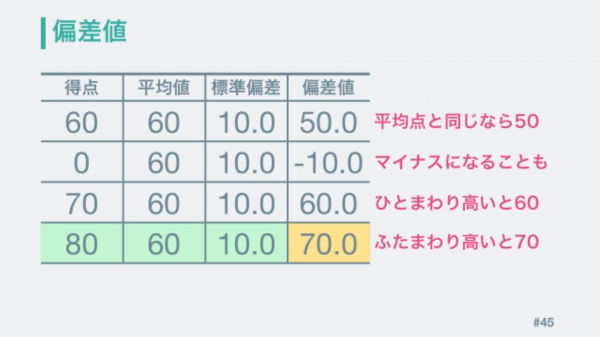
その為、平均点と同じ値をとると偏差値が50になる性質があったり、極端に低い点数だとマイナスになることもあります。得点が平均点よりも標準偏差分だけ高い時は偏差値が60になって、標準偏差の2倍高い時は偏差値が70になるという性質もあります。
こうした偏差値の仕組みの解説にコメント欄では「めちゃくちゃ分かりやすい」「平均が低いテストで高得点をだすと偏差値100超えるからこの数字なんだよってなる」といった意見が寄せられました。
中学数学でわかる偏差値の意味と計算【受験生必見】の解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
▼解説をノーカットで楽しみたい方は
こちらか視聴できます▼
―あわせて読みたい―
・“最強の関数”ってナンだ!? 数式ごとに項を比較して強さを決める動画が登場。n次関数vs指数関数、指数関数vs階乗関数…バトルの結果に視聴者も謎の納得
・「マイナスを引くとプラスになる」を子供に説明できますか? 数学が苦手でも直感的に分かる解説に「なるほど、わかりやすい」