「ミスタードーナツ」のカロリーをあえて数学的に考察してみた! 体積と表面積を演算して導き出した解答に「意味不明だけど面白い」
今回紹介する、AXIONさん投稿の『ドーナツのカロリー変遷』という動画では、音声読み上げソフトを使用し、ミスタードーナツのカロリーについて考察をしていきます。
みなさんは甘いものは好きですか? うp主は好きだけど、カロリーが気になるわよね。で、ドーナツのカロリーとか調べてたら、ドーナツの穴の大きさの変遷が出てきてね。こんなに変わったら正しくカロリー計算できないじゃん……っと調べてみたのね。

まずはドーナツの定義から。ドーナツは図のように半径Rの大円と半径rの小円からなる図形ね。その体積はこんな感じ。要するにドーナツの断面積に全周をかけたものになる。
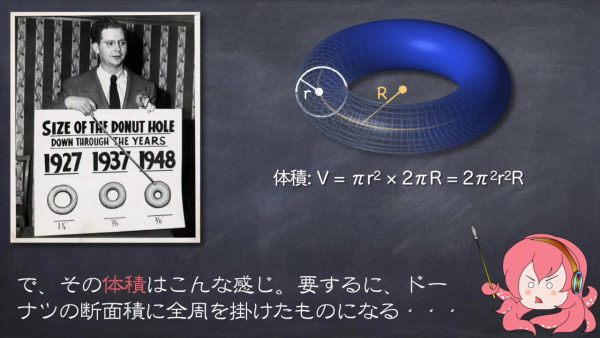
積分計算してもいいけど、ドーナツを輪切りにして、図のように並べれば、直感的にもわかりやすいわね。
で、この写真で手に持っているドーナツが1948年バージョンだとして、テキトーに大きさを仮定してみた。そうするとドーナツの体積が計算できるから、そこからカロリーが……って何か見落としているわね。

ドーナツといってもその形状はいろいろある。そしてトッピングもあるわね。ハニーディップは最もドーナツらしいドーナツなんだけど、表面に砂糖が析出してる。チョコファッションは断面が円ではなく半円で、チョコがちょこっと付いている。
ポン・デ・リングは……まあこの形状が得異だわね。エンゼルクリームは穴がないので今回の考察では出番なし。単にうp主の好みよ。
ちなみにヘリカル型の核融合実験炉みたいな形のドーナツもあるけど、形状が面倒なので今回はパスね。

ではここで考察するにあたって、考慮すべき点をまとめてみる。まず最初に述べたとおり、体積は重要。これに比例してカロリーが増えるはずね。次に表面積も重要。トッピングする場合は、表面積に比例してカロリーが増える。最後は形状ね。体積も表面積も形状に左右される。
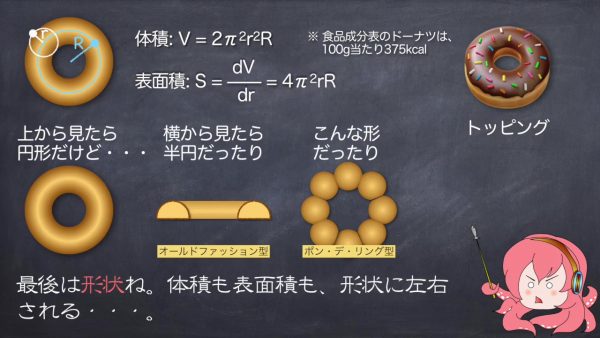
で、まずは形状をこの3つに集約する。「イーストドーナツ型」はここまでの議論で説明した形状……と仮定すると、体積と表面積は既に出てるわね。

「オールドファッション型」はドーナツを水平に半分にした形。体積は半分。表面積は元の半分の面積に断面部分が加わる。でも単純に体積半分だと、重さが半分になる。それでほぼ同じ値段だったら、お客さんが暴動を起こすわね。


仮に半径Rを同じとして体積を同じにすると、今度は「オールドファッション型」のほうが表面積は大きくなるわね。もっと面倒なのは「ポン・デ・リング型」ね。8個ある球体もどきは、2カ所に欠けがある。欠けた部分の体積と表面積はこんな感じ。

前の2つと違い、この形のドーナツが存在するためには、rに下限がある。で、ドーナツの体積と表面積をオラオラっと計算するとこんな感じ。

3つまとめるとこうなる。ただし、「オールドファッション体積問題」とか……比較が難しい。それぞれのカロリーを調べたら、「オールドファッション」がダントツに高い。これは、密度が高いと考えるべきね。実測してみたら、やはり「オールドファッション」は重かったわよ。
ところで、この3種類って、最初の歴史的変遷を経たドーナツ群の穴の大きさと比率が似てない? 3種類のドーナツの外径と内径を4方向から実測して出した結果がこちら。

ここからカロリー密度を定義し、既知のカロリーからこれを算出する。カロリー密度は「オールドファッション」がダントツね。実際、重かったわね。ただし、問題がひとつある。「イーストドーナツ型」にはプレーンがなくて、必ずトッピングがあるのね。
ならばプレーンが実在するドーナツと比較し、面積の差から「仮想プレーン」のカロリーが出せる……。改めて計算し直すとこんな感じ。

次にトッピングのカロリーは「イーストドーナツ型」のバリエーションが参考になる。要するに、表面積の半分に、砂糖、蜂蜜、チョコ、ストロベリーをコーティングした場合の、単位面積当たりのカロリーが計算できる。計算するとこんな感じ。さすがにチョコはカロリー面密度が大きい。
ここまで分かると例えばチョコファッションのチョコに覆われた面積の比率とか計算できるわね。
「オールドファッション型」の場合、平らな部位表面の凸凹が多いので、表面積は計算より大きくなる効果がありそう。そこで平らな部分の疎密係数を定義してみた。これで表面積が増えることになる。

もしかすると「フレンチクルーラー型」も粗密係数を表面積全体にかければ、モデル化できるかも。今後の課題にするわね。
で、ミスド公式からドーナツ種とカロリーをまとめるとこんな感じ。表にすると未発見のドーナツもある。今回の理論値を入れるとこうね。「オールドファッション全がけストロベリー」はとてつもないカロリーになりそうね。何か未発見素粒子を調べているみたいで面白いわよね。

で、結論としては研究のせいで2kg太っちゃったからダイエットしなきゃ。
詳細に解説をしてくださった投稿者さんですが、そのガチ考察にコメントも「難しくておもしろかった!」「意味不明だった(面白かったです)」と盛り上がっていました。解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
・“たこさんウィンナー”はなぜ曲がるのか? 物理と数学の知識を総動員したガチ考察に「なるほど、わからん」
・「鉄1kgと綿1kgどちらが重い?」答えはもちろん…鉄に決まってるw←科学の知識を総動員した“屁理屈理論”に「これはすごい」の声