“たこさんウィンナー”はなぜ曲がるのか? 物理と数学の知識を総動員したガチ考察に「なるほど、わからん」
子供の頃、お弁当に“たこさんウインナー”が入っていると、思わず笑顔になりましたよね? そんなお弁当の定番のたこさんウインナーの足は、なぜあのような形に曲がるのか。
今回紹介する、AXIONさんが投稿した『たこさんウインナー曲率解析』という動画では、音声読み上げソフトを使用して、VOCALOIDの巡音ルカのデフォルメキャラである、たこルカのキャラクターが「たこさんウインナーがなぜあのような形に曲がるのか」について科学の知識で考察を行っています。
ウインナーに切り込みを入れると、なぜ外側に開くのか?
たこルカ:
先日、尻Pのtwitterを見てたらね……美味そうなタコウインナーと一緒に「身の厚みを線形に変化させると、足がサイクロイド【※】になる」という予想が出ててね……。おお……美味しいネタじゃんということで、足の曲率がどうなるかを考察することにしたのね。
※サイクロイド
直線に沿って円が回転するときの円周上の定点の軌跡のこと。
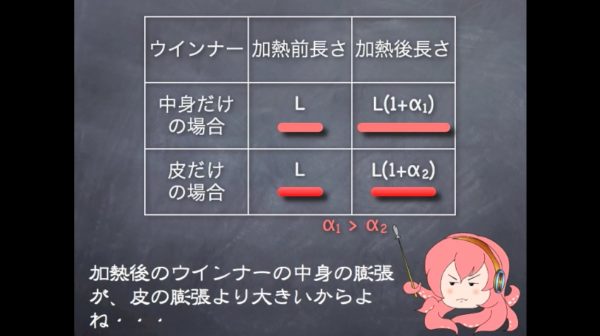
そもそも、ウインナーに切り込みを入れると、何故、外側に開くかを考えると、加熱後のウインナーの中身の膨張が皮の膨張より大きいからよね。

要するに、中身と皮を別々に焼くと、こうなるけど、A面とB面は、本当はくっついているから、中身は縮む方向に力を受け、皮は伸ばされる方向に力を受け、釣り合った長さで止まる。
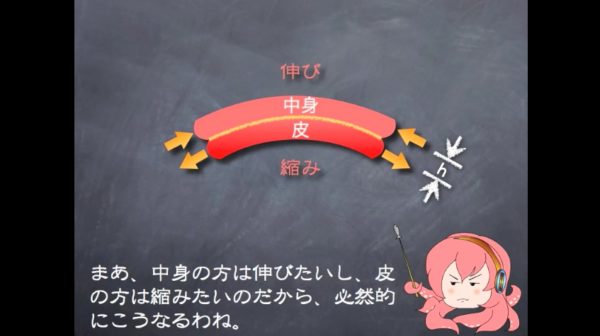
ただし、押す力と引っ張る力は一直線上にないので、偶力【※】となるから、こんな感じで曲がるわけね。まぁ、中身の方は伸びたいし、皮の方は縮みたいのだから、必然的にこうなるわね。
※偶力
作用線が平行で、互いに大きさが等しく、方向が反対向きの2つの力のこと。
ウインナーに切り込みを入れると、加熱後のウインナーの中身の膨張が皮の膨張より大きいからということが分かりました。コメント欄では、「めちゃめちゃわかりやすいww」「皮なしウインナーだと足が開かないって事?」「皮が収縮のような」といったコメントが寄せられました。
たこさんウインナーの曲率は?

たこルカ:
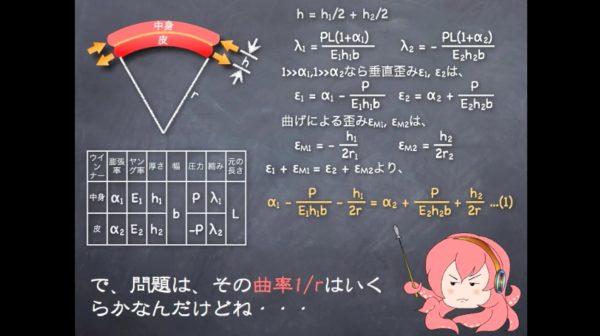
で、問題は、その曲率1/rはいくらかなんだけど……。ここで、変数なのは中身の厚さh₁だけだから……。
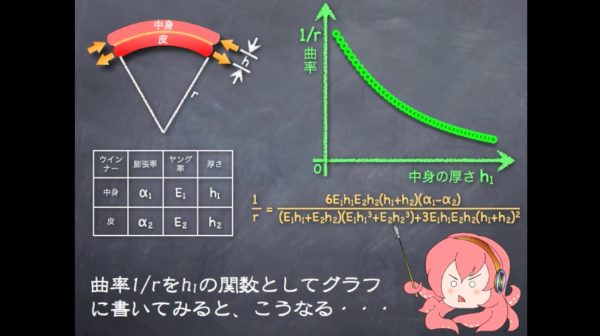
曲率1/rをh₁の関数としてグラフに書いてみると、こうなる。ぶっちゃけ、中身が厚いと曲がり辛いという、当たり前の結論ね。
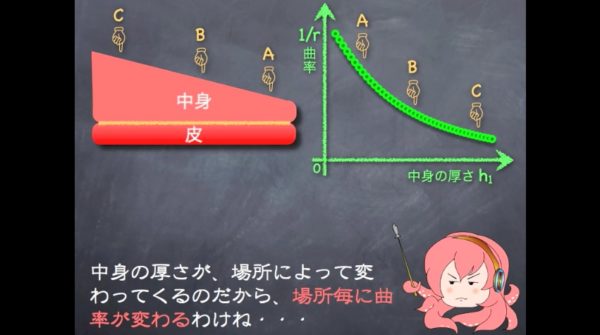
で、実際に知りたいのは、タコウインナーの足がどう広がるかよね。中身の厚さが場所によって変わってくるのだから、場所毎に曲率が変わるわけね。
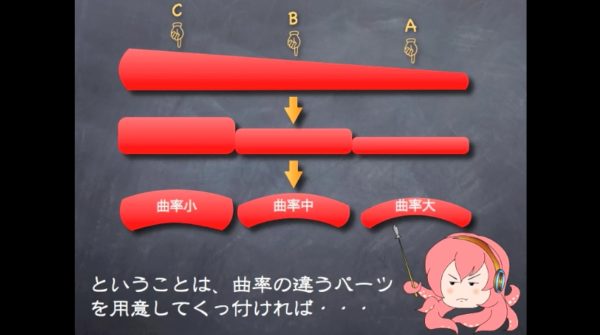
ということは、曲率の違うパーツを用意してくっ付ければ、タコウインナーは再現できる。後はパーツを無限に細かくすれば、数学的にもOK。

ちなみに、中身と皮の厚みが共に厚くなる場合は、曲率は厚みに反比例する。ということで、サイクロイド曲線というよりは、インボリュート曲線【※】に近いわね。と、一応、考察はこれで終わりだけど、ここはやっぱり検証実験すべきよね。
※インボリュート曲線
垂直なベクトルが常に一つの定円に接するような平面曲線のこと。
たこさんウインナーの曲率は厚みに反比例することが分かりました。コメント欄では、「たこさんウインナーこんな数式が・・・」といったコメントが寄せられました。
たこさんウインナーの検証実験してみた結果

たこルカ:
ということで、まず、普通のたこさんウインナー。足は八本よ。次に、ウインナーを三枚に下ろして、中央を斜めに切る。実際に焼いてみるとね、ちょっとずつ曲がってくるのね。

厚みの薄い、先の方から曲がるのが分かるわよね。

タコウインナーも開いてきたわよ。

この辺りが最終形態みたいね。

で、最終的な実験の結論としてはね……ウインナーはビールに限るってことで。
検証実験してみた結果、厚みの薄い、先の方からちょっとずつ曲がるのが分かりました。コメント欄では、「ホントにインボリュートみたいだなぁ」「たこさんウインナーだんだん曲がるから転がるのかw」「するめが曲がったりするのもそういうことなの?」「均等に熱するならゆでたほうが良かったね」といったコメントが寄せられました。
たこさんウインナーの考察をノーカットで楽しみたい方はぜひ動画をご視聴ください。