ケーキとカラースプレーを使って円周率を求めてみた 地道な努力の結果、導き出した円周率に対し「意外と精度いいw」の声
今回紹介するのは、ラムダ技術部 / Yoideaさん投稿の『ケーキを使って円周率を求めてみた』という動画です。
投稿者メッセージ(動画説明文より)
ホールケーキとカラースプレーを用いてモンテカルロ法で円周率を求めてみました。 一般的にコンピュータの中で計算するシミュレーションの手順を現実世界で行うことで親しみを持っていただければ幸いです。
円周率を求める場合、皆さんはどのような方法で求めるでしょうか。
一般的に「円周÷直径」と答える人が多いかと思います。そんな円周率の求め方ですが、世の中には様々な方法が存在します。その中の一つに「モンテカルロ法」と呼ばれる方法が存在します。
簡単に説明するとコンピューターの中で「確率を使って何かを求める」といった計算方法になります。本来はもっと難しい説明が必要なのですが、数式などを見ても理解しづらいと感じる人はかなり多いかと思います。
そんな感覚的に理解しづらい「モンテカルロ法」を、投稿者のラムダ技術部 / Yoideaさんがケーキを使って分かりやすく解説する動画を作成し、その様子を動画で紹介しました。
今回紹介するケーキを使った求め方ですが、非常にシンプルな方法でなんとケーキの上にカラースプレーをランダムにまき散らすだけというもの。一見すると、「それで本当に円周率が求まるの?」と疑ってしまいますが、実際に求まるから不思議です。
モンテカルロ法

初めにケーキに外接するように正方形で囲みます。そして、トッピングなどで使うカラースプレーを50gになるように量ります。

量ったカラースプレーを、ケーキの上でランダムに撒き散らします。ランダムでないといけない為、遠慮せず豪快に撒き散らします。
撒き終わったら、正方形からはみ出したカラースプレーを避けます。正方形とケーキも避けます。

正方形の範囲内でケーキからはみ出たカラースプレーを容器に入れ量ります。ラムダ技術部 / Yoideaさん曰く「少し零しているのは普通にアウトですが、見なかったことにしてください」とのことで、この作業の難しさが伺えます。

測定結果、範囲内ではみ出したカラースプレーは8.83gでした。続いて、範囲外にはみ出たカラースプレーを量ります。こちらの結果は7.38gとなりました。後はこの数値を使って計算するだけで、円周率を求めることができます。

なぜこれだけで分かるかというと、たとえば上の画像の様にランダムに点を置くと、右半分に置かれる確率は2分の1になります。
なぜなら全体の面積に対して右半分の面積も2分の1になるためです。そのため、たくさんの点を置いていくと、右半分に含まれる点の数が全ての点の数の2分の1になります。これが3分の1の面積なら点の比も3分の1になります。
この性質を利用することで、面積が分からない図形でも面積を求めることができます。
とても簡単に言うと、「点を打ちまくれば当たっている部分と当たっていない部分を比べることで面積が分かる」という考え方になります。

今回における円周率πの求め方は、4×(円の内側のカラースプレーの量÷範囲内のカラースプレーの量)で計算することができます。
元のカラースプレーが、50g。
範囲外が、7.38g。
範囲内で円の外側が、8.83g。
全体量から範囲外を差し引くと、範囲内の全体の量が、42.62g。
このことから、円の内側の量が33.79gと分かります。なので、4×33.79÷42.62=約3.17という結果になりました。これはかなり円周率に近い数字です。

カラースプレーをまき散らす際にロスを考えても、十分良い結果が出たとのことです。
ビュフォンの針
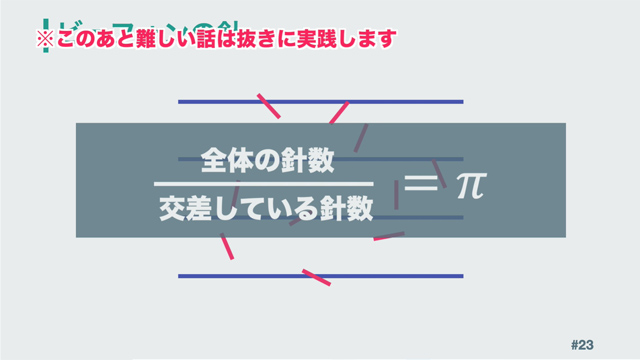
後半は「ビュフォンの針」と呼ばれる方法で円周率を求めます。
やり方は、線の上にたくさんの針を投げて、(全体の針÷線と交差している針の数)で計算するという、これまたシンプルな方法になります。条件として、平行線の間隔を針の長さの2倍にするだけです。
こちらも「そんな方法で求まるのか?」と思う方法ですが、なんと本当に求めることができるそうです。
「よく見るとカラースプレーも針に見えなくもない」ということで、ケーキの時と同じくカラースプレーを使って計算していきます。

ただし、実際行なうとなるとかなり面倒な作業が待っています。なぜかというと今回使用するカラースプレーの数を把握しなければならない為、1本ずつ数える必要があるからです。

面倒な作業を終え、100本のカラースプレーを確保しました。しかし、これでは少ないとのことでもう100本追加で確保することに。

ようやく200本のカラースプレーを数え終えました。数が多ければ多い程精度が増しますが、ラムダ技術部 / Yoideaさん曰く「この先の手順を考えても、あまりに多いと体力が持たないのでこのぐらいで勘弁してください」とのことでした。

等間隔の線の長さを計算するためにカラースプレの平均の長さを調べます。先ほど数えた中から無作為に5本選び計測します。結果、長さの平均が5.92mmでした。
続いて等間隔の線を描くのですが、条件はカラースプレーの2倍の長さが必要なので、5.92×2=11.84mmの間隔で線を描きこみます。

線を描き終えたら、カラースプレーを適当に撒き散らします。ここからとても面倒な「どの線とも交わっていないカラースプレーを取り除き、交わっているカラースプレーの本数を数える作業」を行います。
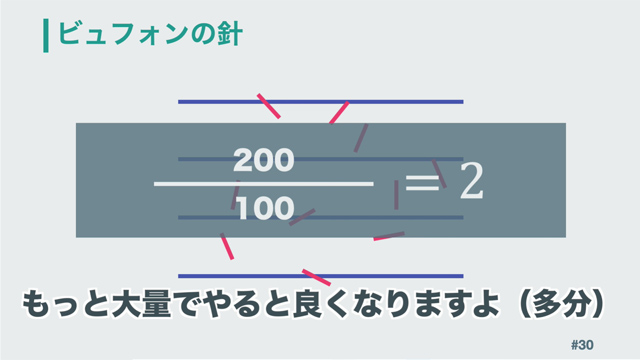
その結果、100本だと分かりました。「ビュフォンの針」の計算式は、(全体の本数÷交差している本数)となり、代入すると200÷100=円周率2となります。今回はちょっと残念は結果になってしまいました。
本数を増やせばさらに精度が高くなるとのことで、この動画を見て興味を持った方は、ぜひチャレンジしてみてはいかがでしょうか。
視聴者のコメント
ランダムが一番難しい
ランダム(むずい)
ケーキよりもパイを買うべきだ
▼動画はこちらから視聴できます▼
―あわせて読みたい―
・大阪万博ロゴ『いのちの輝き』の形をしたポンデリングを作ってみた⁉ その出来栄えに「嫌な予感しかしない」「絶対誰かやると思った」の声