スペースコロニーで野球ってできるの? 落下地点がずれてキャッチャーフライがホームランに!? ボールは壁面へ激突…物理の知識を総動員して計算してみた
スペースコロニーとは、1969年にアメリカの物理学者ジェラルド・オニールらによって提唱された宇宙空間に作られた人工の居住地……「機動戦士ガンダム」シリーズ好きの方には馴染み深いものではないでしょうか。もし、そのスペースコロニーで野球など空間を利用する運動を行うとどうなるでしょうか……?
今回紹介する、AXIONさんは自身が投稿した『スペースコロニーで野球する』という動画で、さまざまな計算式を用いて解説を行います。
第一章 コロニーの設定を確認
今回はニュートン力学【※】の範疇の話題です。まず想定するスペースコロニーは「機動戦士ガンダム」シリーズに出てきたようなシリンダー型。このシリンダーがくるくる回って人工重力を生み出し、その内壁に住むという構造です。
※ニュートン力学
アイザック・ニュートンが、運動の法則を基礎として構築した力学の体系。相対性理論以前の古典力学の体系と見なされる。

もう少し詳しくみていきましょう。コロニーの半径は3km。外周の部分を重力1Gとすると以下のような計算式により、一回転するのに110秒ほどかかるという計算になります。

ちなみに外壁の回転速度は時速617kmにもなるので、コロニー中心から入ったザクが地面に直接降りるとすっ転んでしまいます。

さらに外壁にかかる単位面積あたりの張力Tは、外壁と上の土の遠心力、および1気圧の大気圧に耐えなければいけません。仮にコロニー外敵をステンレス鋼だとし、土の厚さが5メートルなら、外壁の厚さは2メートルは必要です。
現実的に考えると、2メートルの倍の4メートルは欲しいところ。コロニー半径が6.7km以上だとステンレス鋼が回転に耐えきれずちぎれてしまいます。半径3kmというは妥当な大きさとのことです。
時速617kmという日常離れした数値に、「そんな速いのか」「617kmは早すぎだからでかくすりゃいいってもんでもないのか」といったコメントが多数寄せられました。
第二章 ボールの軌道を求めよう
さてここからが本題です。このコロニー内で野球をしたら、打ったボールはどうなるのでしょうか。地球上でボールを真上に打ち上げるとほぼ真下に落ちてきます。ここでいう“ほぼ”というのは、コリオリ力【※】でわずかに曲げられるからです。
※コリオリ力
慣性力の一種であり、地球の自転によって起こる見かけの力のこと。
コロニーの場合、1回転110秒という高速回転なので、コリオリ力の影響は無視できません。また説明を簡単にするため、コロニー内は真空とします。ボールは外からみて仰角θ、初速Vで打ち上げられるとします。このボールは等速直線運動をします。

コロニー内で見ると、ボールの初速と仰角は異なっていて、その軌跡はコリオリ力によって曲がっています。

ここでこのふたつをつなげるためには、静止系と回転系の座標変換の関係式が必要になりますよね。そして静止型からみた実際のボール軌跡を表す運動方程式が必要になります。静止系の運動方程式を回転系に座標変換すればよいので、以下のようになります。

見るからに難易度の高い運動方程式をサクサクと解いていく投稿者に、「!?」「主何者なんだw」といったコメントが寄せられました。
第三章 ボールの着地点を求める
先の章ではボールの軌道を求めていきました。とはいえ先ほどの説明ではあまり腑に落ちない方も多かったのではないでしょうか。理解できたような、できないような……。では次はもう少し具体的に考えていきましょう。
コロニー内でボールを打ち上げた時、ボールの着地点はどうずれるのか? を考えていきましょう。コロニー内でボールを初速V’で打ち上げた場合、たとえそれが真上であってもコリオリ力によって軌道が曲げられてしまうので、出発点と着地点は異なってしまいます。このズレがあまりに大きいと野球をするのは難しいと考えられます。

打ち上げたボールの高さをhとすると、計算式は以下のようになります。

ちなみに高さhを時間で微分すると、鉛直向きのボールの速さが算出できます。

ボールが一番高く上がる時間は、ボールの鉛直速度がゼロになる時で、ボールが着地する時間の半分になります。

ボールの着地点がどれだけずれるかを考えるには、静止系から見た着地点と着地までの時間を考えるとわかりやすいですね。
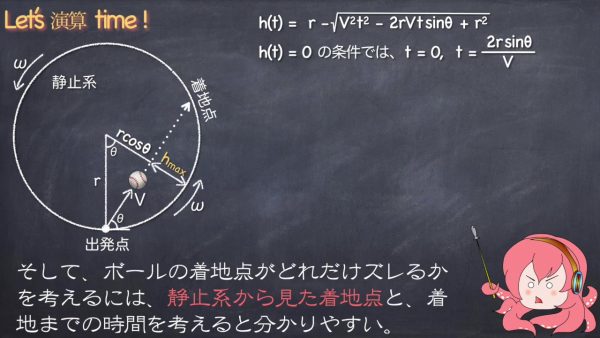
そして静止系からみた出発点と着地点の円弧の距離Liは2θrとなり、出発点は速さrwで回転運動をしているので、回転系から見た円弧の距離Lrでは以下のようになります。
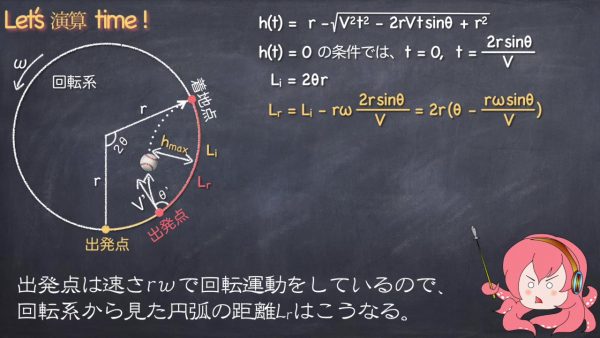
ちなみに回転系上にいる人は(V、ω)はわからないので、(V’、g)との変換式が必要です。
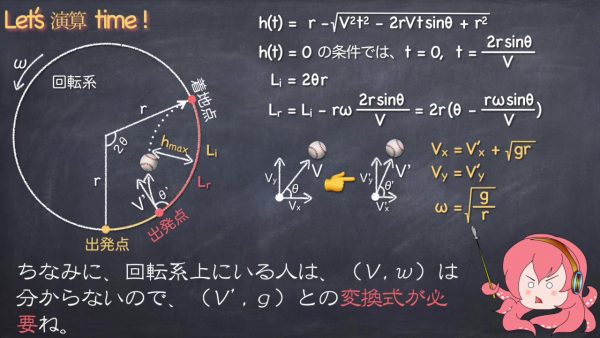
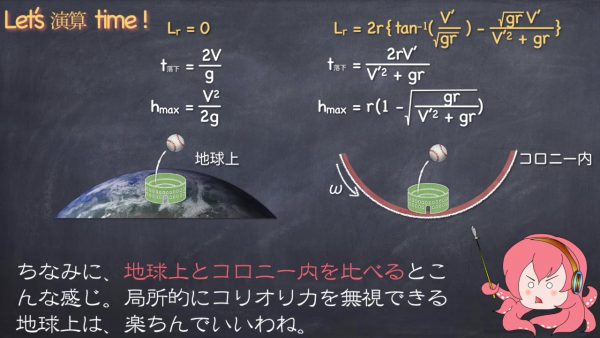
では、ボールを真上に打ち上げた場合の落下点を考えていきましょう。地球上なら打ち上げた場所にそのまま落ちてきます。コロニー上で見た落下地点Lrはこんな感じで求めることができます。

ちなみに地球上とコロニー内を比べるとこんな感じです。
計算式に数値を入れてみるとこんな感じになります。たとえば時速20kmで投げ上げると、1.6メートルまで上がって1.1秒後に落下。落下地点は14センチのずれが発生します。
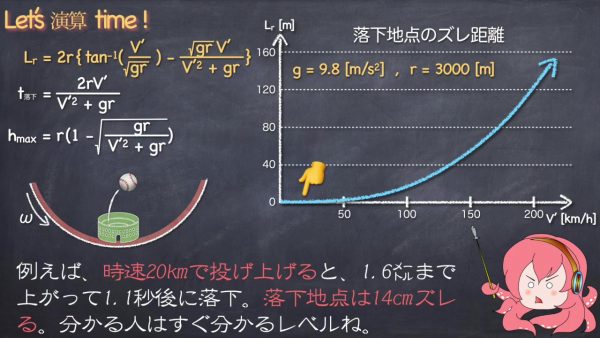
時速100kmだと、39メートルまで上がって5.5秒後に落下。落下地点は16メートルずれます。このずれはわりと大きいですね。
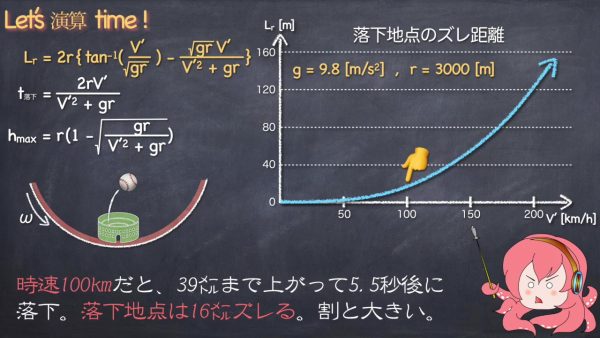
ボールの打球は時速200kmくらいになるので、この場合146メートルまで上がって10秒後に落下。落下地点は121メートルずれてしまう計算になります。
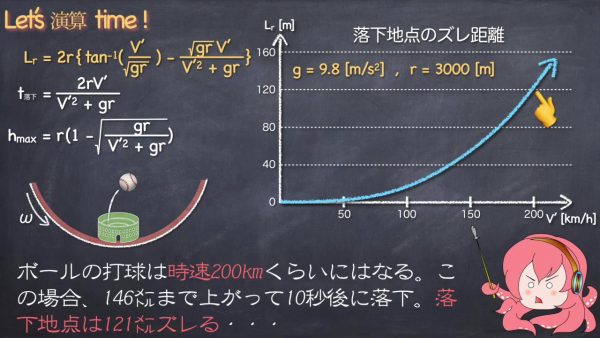
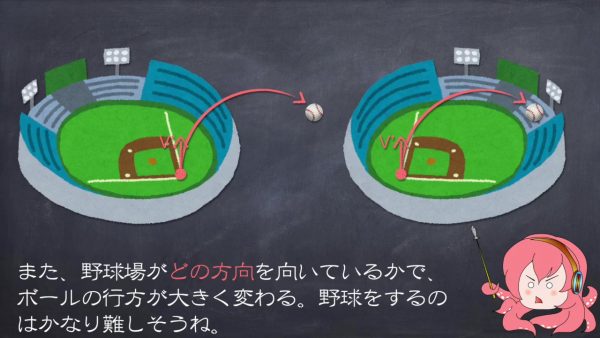
121メートルのずれは、キャッチャーフライがホームランになってしまう計算です。また、野球場がどの方向を向いているかでホームランになるのかファールボールになるのか大きく変わってしまいますので、野球をするのはかなり難しいだろうという結論になりました。
地球上とコロニーで打ち上げられた物体の落下時間と最高速度の違いをグラフで示すと、このようになります。
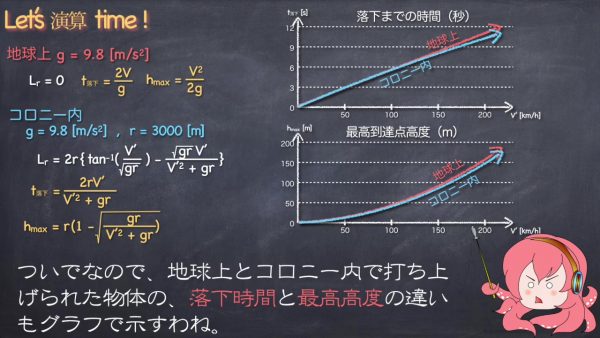
あれ、あまり変わらない……? と思いますが、実はボールの速さが遅いからなのです。ボールの速さを時速1300km程度のマッハ1くらいまで上げると、このようになります。
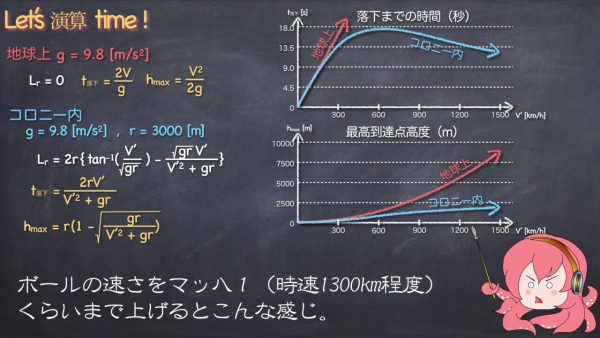
ボールの速さが時速600kmを超えるあたりから、落下時間が短くなるところが面白いですね。ここまで速いと、さすがに落下というより側面への激突となってしまいますが……。そしてコロニー内では最高速度が伸びません。なぜならコロニー内での最高地点が高度3000メートルだからということです。
ボールの軌道や落下地点が地球とではまったく違うという予測に、「現地の人なら暮らしてるうちに独自の物理法則を経験で理解してそうね」「逆にコロニー生まれは地球の物理を変なの! って思うんだろうなぁ」「コロニー内で公平性を考慮したスタジアムの設計がどうなるかきになる」「つまりニュータイプはコリオリの力を極めた者だった・・・!?」といった様々なコメントが寄せられました。
解説をノーカットで楽しみたい方はぜひ動画をご視聴ください。
ーあわせて読みたいー
・「なぜ0で割ってはいけないの?」 数学マニアが中学生にもわかるようにした解説がエレガントすぎると話題に
・漫画やアニメでお馴染み“炎のシュート”を蹴るにはどうすればいいのか? マッハ2.9、ライフル弾並みのスピードを受け止めるキーパーって一体